probablemente haya problemas de lectura con los símbolos matemáticos. AQUÍ TIENES EL PDF.
Tenemos que reconocer que como especie sentimos un muy especial atractivo a aquello que no somos capaces de comprender. Quedamos por ejemplo, maravillados con la sorpresa que nos produce un truco de magia. Luego, cuando nos explican el cómo, ya no era para tanto. Podríamos decir, que encontramos más placer en el «engaño» que en el entendimiento. Nos encanta relacionar aquello que se escapa a nuestra comprensión, con el misticismo. Solemos, con frecuencia, achacar a los deseos, claros u oscuros, de algún dios, de algún ente superior, la perfección del mecanismo al que atienden ciertos comportamientos que no sabemos explicar. Esto ha sucedido siempre y, por supuesto, sigue sucediendo a día de hoy, en el evolucionado siglo XXI.
Si hay algo dentro de las matemáticas, que se haya hecho popular por esta razón, es todo aquello relacionado con la proporción áurea. El número de oro, y todo lo que de alguna manera se pueda vincular con él, ha estado históricamente ligado a conceptos subjetivos, místicos y religiosos. La sucesión de Fibonacci, la espiral áurea y la propia proporción, a causa de sus innumerables propiedades, han sido siempre causa de sorpresa, asombro y maravilla, y esto ha derivado en que su existencia se asocie a algo más poderoso que lo humano, es decir, a lo divino. Ya Luca Pascioli, alrededor del 1500, etiquetó a esta razón como «divina proporción» arguyendo para ello 5 razones: 1) la proporción es única como dios es único; 2) la proporción se define a partir de tres segmentos de recta al igual que la santa trinidad; 3) la proporción es inconmensurable (irracional) como dios es inconmensurable (¿irracional?); 4) la proporción tiene propiedades de autosimilaridad que se relacionan con la omnipresencia de dios; y 5) la proporción está muy presente en el dodecaedro **es con este sólido con el que (según los platónicos) se representa la quintaesencia (digamos que según Platón, la quintaesencia es el alma del universo) que representa la existencia de dios**.
¿Cómo se define la proporción? Lo más sencillo aquí es dar la definición que aparece en los Elementos de Euclides: «Se dice que una recta ha sido cortada en extrema y media razón cuando la recta entera es al segmento mayor como el mayor es al menor». Esto es sencillamente, que si cortamos una recta en dos segmentos debe cumplirse que
$$\frac{Longitud\ Segmento\ Mayor}{Longitud\ Recta}=\frac{Longitud\ Segmento\ Menor}{Longitud\ Segmento\ Mayor}$$
que podemos traducir en que si tenemos dos segmentos de longitudes $a$ y $b$ ($a>b$), entonces
$$\frac{a}{a+b}=\frac{b}{a}$$
Una definición inocente y un juego geométrico casi recreativo. Cabe recordar, que en la antigua Grecia, una proporción era a menudo representada por la progresión que generaba. Así, si denotamos por $\phi=\frac{a}{a+b}=\frac{b}{a}$ (es decir, la razón áurea), esta misma proporción podría definirse como la progresión geométrica que genera: $1,\ \phi,\ \phi^2,\ \phi^3,…$.
Y ahora Fibonacci. Leonardo da Pisa vivió rondando el 1200 (300 años antes de que Pascioli se flipara con lo de «divina») y, cosas de la vida, tuvo mucho roce con culturas árabes, de donde aprendió muchas cosas (que esta gente traía sabidas principalmente de la India) y gracias a eso los occidentales dimos un estirón en esto de las matemáticas. Su contribución más importante es introducir el sistema decimal en Europa. Sin embargo, por lo que su nombre suena y resuena, es por una sucesión (que también era ya conocida en la India, aunque esto es lo de menos) que ha terminado llevando su nombre. En el Liber Abaci, Fibonacci propone un problema, de nuevo casi de forma recreativa, sobre la cría de conejos. Y es este problema el que lo ha traído a la fama. No entraremos en detalles sobre el problema y su solución (ya está bastante trillado, verdad?). La cuestión es que, la sucesión de Fibonacci (parejas de conejos a lo largo del tiempo), quedaría como
$$0,\ 1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,…$$
Esta sucesión se genera a partir de dos semillas o valores iniciales, $0,\ 1$, y cada término de la sucesión se obtiene sumando los dos inmediatamente anteriores. Formalmente tendríamos
$$
\left \{
\begin{array}{rcl}
F_0 & = & 0 \\
F_1 & = & 1 \\
F_n & = & F_{n-1}+F_{n-2}
\end{array}
\right .
$$
La sucesión de Fibonacci es tremendamente famosa por tener muchas propiedades, en un principio, recreativas. Por ejemplo, $$F_n=\frac{F_{n-2}+F_{n+1}}{2}\ \ (1)$$
que dice que hacer el promedio de dos términos de la sucesión que estén separados por tres grados de distancia, nos da un segundo grado desde el menor; algo así como, $\frac{2+8}{2}=5$ ó $\frac{8+34}{2}=21$.
$$F_0+F_1+F_2+F_3+…+F_n=F_{n+2}-1\ \ (2)$$
que viene a decir que sumando todos los términos de la sucesión hasta uno arbitrario, y sumamos uno al resultado, nos dará otro término de la sucesión (el que hace dos). Algo así como, $1+1+2+3+5=13-1$; ó, $1+1+2+3+5+8+13=34-1$. ¿Hay más? A montones,
- $F_0-F_1+F_2-F_3+…+(-1)^nF_n=(-1)^nF_{n-1}-1$
- $F_1+F_3+F_5+…+F_{2n-1}=F_{2n}$
- $F_0+F_2+F_4+F_6+…+F_{2n}=F_{2n+1}-1$
- $F_0^2+F_1^2+F_2^2+F_3^2+…+F_n^2=F_{n}F_{n+1}$
- $F_0F_1+F_1F_2+F_2F_3+F_3F_4+…+F_{2n-1}F_{2n}=F_{2n}^2$
- $F_n^2+F_{n+1}^2=F_{2n+1}$
- $F_{n+2}^2-F_{n}^2=F_{2n+2}$
- $F_{n+2}^2-F_{n+1}^2=F_{n}F_{n+3}$
- …
(nótese aquí que nuestro interés está en los cocientes para $n$ indefinidamente grande, por lo que el cociente entre los dos primeros términos no esté definido aritméticamente no es ningún problema aquí).
¿Por qué esta propiedad eclipsa a los cientos de propiedades que tiene esta sucesión? No lo se. Mi hipótesis es que quizá, nos resulta intuitivo, que la sucesión, tal cual se define, es decir, de forma aditiva, pues deriva en este tipo de propiedades; al fin y al cabo, lo que envuelven, son sumas y restas. Por ejemplo, simplemente partiendo de la definición $F_n = F_{n-1}+F_{n-2}$, y sumando a ambos lados de la igualdad, $F_n$, nos quedará, $2F_n = F_n+F_{n-1}+F_{n-2}$, pero además, como $ F_{n}+F_{n-1}=F_{n+1}$, pues nos queda que, $2F_n = F_{n+1}+F_{n-2}$, y de ahí tenemos la propiedad que en (1) interpretábamos como un promedio de términos de la sucesión. Lo que un poco más arriba, anotamos como propiedad (2), intuimos que será bastante sencillo de demostrar por inducción, y si no conocemos ésta herramienta, pues por la cuenta la vieja también nos valdrá; sustituyendo sucesivamente valores en la expresión de la derecha del igual y simplificando la expresión. Y así con todas. Entretenido pero sencillo. Sin embargo, quizá no nos resulte tan intuitivo, que el límite de los cocientes acabe en $\phi$. Esto es lo que quiero esforzarme en pensar. Pero si soy completamente honesto, no puedo dejar de sospechar, que la inercia al misticismo de la que hablábamos al principio, es la que hace que se nos pongan los pelos de punta, justo cuando vemos $\phi$, y no antes.
Generalización. Todas estas propiedades que acabamos de nombrar, no son exclusivas de la sucesión de Fibonacci, sino que se deben a ésta forma aditiva en que es definida la sucesión. Es decir, la sucesión de Fibonacci es solo un caso particular, y en general, cualquier sucesión de la forma $a_n = a_{n-1}+a_{n-2}$, cumplirá con estas propiedades, independientemente de los valores “semilla” que decidamos para $a_1$ y $a_2$ (las dos pruebas arriba para las propiedades (1) y (2) en ningún momento han necesitado de valores iniciales; y lo mismo sucede para todas las demás). A cualquier sucesión definida de esta manera se le suele denominar sucesión áurea, y los nombres particulares vienen cuando definimos valores iniciales. Los más conocidos son, como ya hemos dicho, los que generan la sucesión de Fibonacci ($a_1=1$ y $a_2=1$), pero también goza de cierta fama la sucesión de Lucca ($a_1=1$ y $a_2=3$). ¿Por qué sucesión áurea? Pues claramente a causa de la propiedad estrella, porque siempre sucede, recalcamos que independientemente de los valores iniciales, que $$\lim_{n \to \infty}\frac{a_{n+1}}{a_n}=\phi.$$ **Quizá has notado algo raro, en cuanto al recorrido de los subíndices, al generalizar desde la sucesión de Fibonacci, $F_n$, a esta sucesión áurea, $a_n$. Da igual, ¿no?.**
Paréntesis. Podemos determinar un valor aritmético para esta proporción traduciendo la igualdad, $$\frac{a}{a+b}=\frac{b}{a},$$ a un lenguaje algebraico que nos resulte útil para nuestro interés. Algo así, como crearnos la escala de un mapa. $a$ es a $a+b$ lo que $b$ es a $a$, y para hacer la escala diremos, lo que $1$ es a $x$, por lo tanto, reescribimos $b=1$ y $a=x$, de donde $$\frac{x}{1+x}=\frac{1}{x}.$$ Multiplicando en cruz, obtenemos $$x^2=1+x,$$ que da lugar a la ecuación de segundo grado que resuelve el valor aritmético de nuestra idolatrada proporción $$x^2-x-1=0.$$ Pero no nos interesa esta ecuación, sino más bien nos quedaremos en la expresión $x^2=1+x$. Como hemos quedado en llamar a nuestra razón dorada $\phi$, y además, resulta que $\phi$ es la solución de esta ecuación, pues sucede que $\phi^2=\phi+1$. Ahora, simplemente multiplicando ambos lados de la igualdad por $\phi$, obtendremos $\phi^3=\phi^2+\phi$. Si procedemos recursivamente, es obvio que $$\phi^n=\phi^{n-1}+\phi^{n-2}.$$ Por lo tanto, la progresión del tipo geométrico (cada término se obtiene multiplicando su anterior por una razón), que decíamos que los griegos ya utilizaban para describir la proporción, ha resultado ser también, una sucesión de las del tipo que hemos llamado áureas, y que se puede generar aditivamente.
¿Hay conexión?. Claro, ya hemos dicho que la sucesión de Fibonacci es un caso particular de sucesión áurea. Esto lo podemos deducir, además, desde otro punto de vista. ¿Qué pasa si intentamos obtener directamente el valor de $a_n$ a partir de los valores de las semillas $a_1$ y $a_2$?. Procedemos recursivamente. Sabemos que $a_n = a_{n-1}+a_{n-2}$, por lo que $a_3= a_2+a_1$, y $a_4= a_3+a_2$. Sustituimos el valor de $a_3$ de la primera igualdad en su correspondiente de la derecha de la segunda igualdad, por lo que $a_4= ( a_2+a_1)+a_2=2·a_2+a_1$. Otra vez. Como $a_5= a_4+a_3$ y ya tenemos $a_4$ y $a_3$ en función de las semillas, podemos sustituir y tenemos $a_5= (2·a_2+a_1)+(a_2+a_1)=3·a_2+2·a_1$. ¿Aun no? Hacemos otra. $a_6= a_5+a_4=(3·a_2+2·a_1)+(2·a_2+a_1)=5·a_2+3·a_1$. Ahora seguro que si. Si necesitas un poco más no te preocupes, puedes ejecutar un par de pasos más y te vas a dar cuenta de que $$a_n=F_{n-1}·a_2+F_{n-2}·a_1.$$ Ou, yeah!! Así que la sucesión de Fibonacci no es más que un caso particular de la sucesión áurea en el que las semillas son el elemento neutro del producto!!! **cuidado, las semillas de la sucesión áurea, la de términos $a_n$**.
Volvamos a $\phi^2=\phi+1$. De aquí surgen dos propiedades maravillosas de la proporción áurea. La primera es, que si aplicamos raíz cuadrada a ambos lados de la igualdad tenemos que $\phi=\sqrt{1+\phi}$, y si ahí vamos sustituyendo el $\phi$ de la izquierda en el $\phi$ de la derecha tenemos que $\phi=\sqrt{1+\sqrt{1+\phi}}$, y otra vez $\phi=\sqrt{1+\sqrt{1+\sqrt{1+\phi}}}$, y otra, y otra, y otra,…$$\phi=\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+…}}}}}$$ De esta propiedad nos olvidaremos en este artículo. Nos vamos a centrar en la que viene a continuación. La construimos de forma muy parecida, pero en lugar de aplicar raíz cuadrada, dividimos ambos lados de la igualdad por $\phi$, de forma que $\phi=1+\frac{1}{\phi}$. Igual que acabamos de hacer con la raíz, vamos sustituyendo el $\phi$ de la izquierda en el $\phi$ de la derecha, y lo hacemos indefinidamente, y obtenemos $$\phi=1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+…}}}}$$
Esto es bellísimo, pero es mucho más. Es la expresión de $\phi$ como fracción continua. Una fracción continua, que además esta formada únicamente por unos, lo que implica que $\phi$ es el número irracional que más lentamente converge a un número racional, es decir, que $\phi$ es el número más irracional.
¿Por qué $\frac{a_{n+1}}{a_n}\longrightarrow \phi$? Hemos visto que la progresión geométrica generada por $\phi$ se puede obtener también de forma aditiva, consiguiendo cada término $a_n$, a partir de las semillas $a_0=1$ y $a_1=\phi$. Obviamente, para este caso particular sucede que $\lim_{n \to \infty}\frac{a_{n+1}}{a_n}=\lim_{n \to \infty}\frac{\phi^{n+1}}{\phi^n}=\phi$. ¿Que pasa para el caso general? Utilizando la definición de $a_n$, tenemos que $a_{n+1} = a_{n}+a_{n-1}$, de donde $$\frac{a_{n+1}}{a_n}=\frac{a_{n}+a_{n-1}}{a_n}=1+\frac{a_{n-1}}{a_n}=1+\frac{1}{\frac{a_{n}}{a_{n-1}}}$$ y ahora debemos proceder de forma análoga sobre la fracción $\frac{a_{n}}{a_{n-1}}$. Tenemos de esta manera, que cuando $n$ se hace indefinidamente grande, $$\frac{a_{n+1}}{a_n}=1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{…}}}}$$ que es la fracción continua que decíamos representa el valor de $\phi$. Si te resulta más sencillo, puedes construir la fracción continua andando el camino inverso. Puedes empezar con el hecho de que $\frac{a_{2}}{a_1}=1$. Luego puedes hacer $$\frac{a_3}{a_2}=\frac{a_2+a_1}{a_2}=1+\frac{a_{1}}{a_2}=1+\frac{1}{\frac{a_2}{a_1}}=1+\frac{1}{1},$$ y luego pues $$\frac{a_4}{a_3}=\frac{a_3+a_2}{a_3}=1+\frac{a_{2}}{a_3}=1+\frac{1}{\frac{a_3}{a_2}}=1+\frac{1}{1+\frac{1}{1}},$$ y así hasta que te aburras. De nuevo, en el infinito, te vas a reunir con $\phi$.
Juega conmigo. Queda demostrado que la «magia» no es de la sucesión de Fibonacci, sino de cualquier sucesión que generemos de forma recursiva, utilizando esta regla aditiva de obtener cada elemento, sumando los dos inmediatamente anteriores. ¿Quieres probar? Inventa dos números, digamos el $5$ y el $3$ (elige los tuyos), y ahora genera tu propia serie de la forma en que hablamos, en este caso, $5,\ 3,\ 8,\ 11,\ 19,\ 30,\ 49,\ 79,…$ y después, la serie de cocientes consecutivos $$\frac{3}{5},\ \frac{8}{3},\ \frac{11}{8},\ \frac{19}{11},\ \frac{30}{19},\ \frac{49}{30},…$$ Toma la calculadora, ve dividiendo, y mira a ver si diera la casualidad de que el resultado se va aproximando, cada vez más y más, a $\phi$. Ah, vaya despiste, $\phi$ es aproximadamente $1.618$.
Más mitos de la sucesión de Fibonacci. Elige cuatro términos consecutivos de la sucesión de Fibonacci, multiplica los extremos, calcula el doble del producto de los medios, suma los cuadrados de los medios. Tachan!! Obtenemos una terna pitagórica. Bien, esto quizá te parece un trabalenguas enredado. Vamos a entendernos utilizando los números. Elegimos cuatro términos consecutivos de la sucesión de Fibonacci arriba. Por simplificar los cálculos $1,\ 2,\ 3,\ 5$ pero te invito a que repitas esto con tu propia elección. Por un lado $1\cdot5=5$, por otro lado $2·2·3=12$, y por otro $2^2+3^2=13$. Y si, sucede que $5^2+12^2=13^2$. Y sucede cualesquiera cuatro términos que seleccionemos mientras que estos sean consecutivos. Pero según lo dicho hasta ahora, esto huele a no ser una propiedad exclusiva de la sucesión de Fibonacci. ¿No será esto consecuencia directa de la forma en que tenemos de construir esta sucesión? es decir, esto se debe a que $a_{n+1} = a_{n}+a_{n-1}$. Simplificando la notación, podemos decir que cuatro términos consecutivos de la progresión serían $x$, $y$, $x+y$, y $x+2y$ ($y \geq x$). El producto de los extremos queda $x(x+2y)$ y el doble del producto de los medios $2y(x+y)$. La suma del cuadrado de los medios quedaría $x^2+(x+y)^2$. Tomamos esta última y desarrollamos un poco $$y^2+(x+y)^2=y^2+x^2+y^2+2xy=y^2+y^2+xy+x^2+xy=y(x+2y)+x(x+y)$$. Esto explica otra versión del enunciado que modifica la suma del cuadrado de los medios, por la suma de los productos de los términos de posición impar y los de posición par (es decir, en lugar de $2^2+3^2$ en nuestro ejemplo, haríamos $1·3+2·5$). El objetivo es demostrar que ($x(x+2y)$, $2y(x+y)$, $x^2+(x+y)^2$) forman una terna pitagórica, es decir, la suma del cuadrado de los dos primeros, da como lugar el cuadrado del tercero. Volvemos a tomar el tercer término y volvemos a jugar con él, tal y como hemos hecho hace un momento:
¿No es este enunciado mucho más espectacular? Nos libera de tener que elegir los números de entre una sucesión concreta pudiendo elegirlos a nuestro antojo. Entonces, ¿por qué recurrimos a Fibonacci?:
Misticismo matemático & Business is business. Fibonacci vende.
Pero, ¿no encontramos la sucesión de Fibonacci frecuentemente en la naturaleza? Como hemos visto, la sucesión de Fibonacci es un caso particular de sucesión áurea, y además, no sería descabellado pensar en que un proceso natural (o no) se propague como esta sucesión se propaga. En realidad, la sucesión de Fibonacci, nace de un problema que plantea este señor en el Libber Abaci en 1202 y que resulta muy ilustrativo del trasfondo en este tipo de crecimiento. El problema dice (casi) textualmente ¿Cuántas parejas de conejos tendremos a fin de año si comenzamos con una pareja que cría cada mes otra pareja que puede empezar a procrear a partir de los dos meses de vida? Digamos que una pareja de conejos deja descendencia cada mes (una pareja de bebes). Esta nueva pareja necesita madurar para poder procrear, y en esto tarda un mes. Es decir, tenemos una pareja $a_1=1$. Un mes para madurar, $a_2=1$. Ahora ya empiezan a procrear, por lo que el siguiente mes tendremos la pareja original y sus hijos, $a_3=2$. Los padres pueden procrear cada mes, pero los hijos están madurando, por lo que $a_4=3$. Ahora tenemos: la pareja original, que sigue procreando, la primera pareja de crías, que ya ha madurado y puede procrear, y la segunda pareja de crías, demasiado jóvenes, por lo que $a_5=5$. En general, para saber la cantidad parejas que tenemos en un mes $n$ tenemos que añadir a la cantidad de parejas que teníamos el mes anterior $n-1$, una nueva cantidad de crías correspondiente a las parejas que son suficientemente maduras como para criar, es decir, las que tienen al menos dos meses de vida, es decir, las que teníamos hace dos meses $n-2$. Por lo tanto, $a_n=a_{n-1}+a_{n-2}$. Todo tiene sentido, salvo que los conejos no procrean de esta manera. Sin embargo, si resulta ilustrativo de un proceso de expansión en el cual se van acumulando fuerzas productivas después de esperar cierto tiempo de maduración. Por lo tanto, no ha de sorprendernos encontrar este tipo de crecimiento en ciertos fenómenos naturales. Eso sí. Muchas menos veces de lo que la propaganda ha hecho que se perciban en la imaginativa popular. Ya hemos dicho que los conejos no se reproducen de esta manera.
¿Dónde si?. En el árbol genealógico de un zángano. Sucede que los huevos de las abejas obreras no fertilizados evolucionan a zánganos, por lo que los zánganos no tienen padre pero si tienen madre. Pero las hembras si tienen dos progenitores, por lo tanto, un zángano (1) tiene una madre (1) que tiene un padre y una madre (2), el padre tiene madre y la madre tiene padre y madre (3), la madre del padre y la madre de la madre tienen ambos madre y padre, pero el padre de la madre solo tiene padre (5), y si quieres, puedes seguir con este trabalenguas tan entretenido. Mira:
También sucede, que en filotaxis se ha solido explotar la idea de sucesión de Fibonacci y, cuando esta falla, sucesión de Lucas (sucesión áurea con las semillas $a_1=1$ y $a_2=3$). Aquí, con el tiempo, se ha demostrado que no es tanto la sucesión, sino su convergencia a la proporción. Ya hemos visto que el número de oro es el más irracional de todos, el que más lentamente converge a un número racional.
¿Entonces lo que vemos es el número de oro? La proporción áurea tiene una presencia significativamente mayor que la sucesión de Fibonacci en la naturaleza. Como acabamos de decir en el párrafo anterior, se encuentra aproximadamente en el ángulo que forman los tallos de una planta entre sí, o en las pipas de un girasol o de una piña. En general, suele estar presente en el proceso de crecimiento de muchas plantas. Esto tiene una explicación perfectamente racional. Hemos dicho que $\phi$ es el número más irracional, por lo que cuanto más cerca estemos de esta proporción, más lejos estaremos de solaparnos (en caso de ser tallos y necesitar de la luz del sol y del agua de la lluvia) o nos permitirá ocupar el espacio de forma más óptima (si somos, por ejemplo las pipas en la flor de un girasol). Además, atendiendo a la definición original «la parte pequeña es a la grande como la parte grande es a la suma» podemos decir que es el número que permite mantener la proporcionalidad entre las partes y el todo. Quizá sea por eso tan frecuente en anatomía. El número de oro está presente como proporción en el pentágono, y la simetría pentagonal está presente en muchos elementos de la naturaleza. Muchas flores tienen 5 pétalos (diría que es bastante falaz que la cantidad de pétalos de una flor es un número de Fibonacci, pero allá cada cuál). Las personas tenemos 5 extremidades (si nos colocamos como Vitrubio quiere, empezaremos a encontrar el número de oro por todas partes)… de ahí, que podamos seguir encontrando aproximaciones de $\phi$, si miramos con los ojos adecuados.
¿Y qué me dices de la espiral dorada? Sí. Vemos espirales logarítmicas por todos lados. Lo que no vemos son espirales doradas, aunque a menudo confundimos (por nuestro propio pié o inducidos), espiral logarítmica con espiral dorada. Hemos dicho que $\phi$ genera una progresión que es geométrica, y, por definición, una espiral logarítmica es una espiral en la que el radio aumenta de forma exponencial (geométrica). La espiral dorada vuelve a ser sólo un caso particular, esta vez, de una espiral logarítmica (la de razón $\phi$). El ejemplo más trillado de número áureo en la naturaleza en forma de espiral es el de la concha del Nautillus. Pues bien, sí que se trata de una buena aproximación a una espiral logarítmica, pero de razón cercana a $1.2$, que queda muy lejos de cualquier aproximación de $\phi$. Hay un libro llamado The curves of life de T.A. Cook que muestra la extraordinaria presencia de esta espiral (la logarítmica) en la naturaleza. ¿Por qué decide la naturaleza seguir esta trayectoria? Pues porque cualquier espiral logarítmica tiene dos propiedades que resulta importantísimas en este sentido. La primera es, que la superficie delimitada por ángulos iguales, aumenta siempre en la misma proporción (lo que hace que un molusco, que va haciendo crecer su caparazón a la misma velocidad que va creciendo él, encuentre su casa exactamente igual en todas las fases de su desarrollo, lo que le permite no desorientarse nunca), y la segunda, es que es una espiral equiangular (un halcón a la caza desciende en espiral, porque para mantener la máxima velocidad necesita mantener la cabeza fija, y entonces, para mantener a su presa siempre a la vista sigue -quizá sin saberlo- esta trayectoria). En ninguno de los dos ejemplos la espiral tiene por qué ser dorada.
De hecho, ¿sabemos distinguir una espiral dorada? Escribiendo esta entrada me he cuestionado si realmente somos capaces de distinguir, a simple vista, la proporción. Me he creado un par de espirales y las he pasado por estas encuestas express que nos permite instagram y facebook. ¿Cuál es una espiral dorada? a) 61 % b) 39% (es verdad que sólo 28 participantes). ¿Cuál ves más proporcionada? a) 69% b) 31% (776 participantes!!).
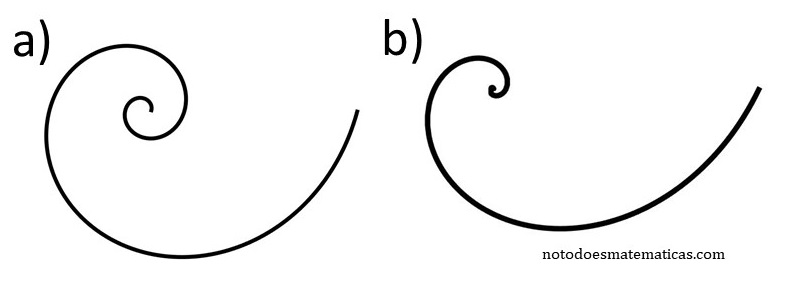
Llegados a este punto espero no haberte roto el corazón. La magia no existe. Las matemáticas si. Sospecha. Duda. Razona. Kill your idols.
